Suppose that you knew a Maclaurin series for a function \(f(x)\) but you need the series for \(1/f(x)\), valid for small values of \(x\). For example, we know the series for \(\cosh x\) from the above list (or we could derive it ourselves). The hyperbolic secant function, \(\sech x = 1 / \cosh x\). How could we compute the series for \(\sech x\), valid for small \(x\) through terms of order \(x^6\)?
The “easy” way is to go back to the definition of the Taylor series and work out all the derivatives of \(\sech(x)\). While this is straightforward, in principle, the expressions for the derivatives get more and more complicated as we proceed. [If you don’t believe me, try it!]
Here’s another option. For small \(x\), \begin{equation} \cosh x = 1 + \underbrace{\frac{x^2}{2!} + \frac{x^4}{4!} + \frac{x^6}{6!} + \cdots}_{q} \end{equation} where \(q\) is a “small quantity” as long as \(x\) isn’t too large. So, \begin{equation}\label{eq:sech1} \sech x = \frac{1}{\cosh x} = \frac{1}{1 + q} = (1 + q)^{-1} \end{equation} But, the binomial series for \(n = -1\) is just \[ \frac{1}{1 + q} = 1 - q + q^2 - q^3 + \cdots \] To produce the series for \(\sech x\) valid for terms through \(x^6\) just requires us to keep all the terms in \(-q + q^2 - q^3\) through \(x^6\). We’ll work term by term: \begin{align} -q &= -\frac{x^2}{2!} - \frac{x^4}{4!} - \frac{x^6}{6!} - \frac{x^8}{8!} + \O{x^{10}} \notag \\ q^2 &= \frac{x^4}{(2!)^2} + 2 \frac{x^2 \; x^4}{2! \; 4!} + 2 \frac{x^2}{2!} \frac{x^6}{6!} + \left( \frac{x^4}{4!} \right)^2 + \O{x^{10}} \notag \\ &= \frac{x^4}{4} + \frac{x^6}{4!} + x^8 \left( \frac{1}{6!} + \frac{1}{(4!)^2} \right) + \O{x^{10}} \notag \\ -q^3 &= -\left(\frac{x^2}{2!} \right)^3 - 3 \left(\frac{x^2}{2!}\right)^2 \frac{x^4}{4!} + \O{x^{10}} \notag \\ q^4 &= \frac{x^8}{16} + \O{x^{10}} \notag \end{align}
Now, we just need to combine all these terms: \begin{align} \sech x &= 1 - \frac{x^2}{2} + x^4 \left( -\frac{1}{4!} + \frac{1}{4} \right) + x^6 \left( -\frac{1}{6!} + \frac{1}{4!} - \frac{1}{8} \right) \notag \\ &\qquad + x^8 \left( -\frac{1}{8!} + \frac{1}{6!} + \frac{1}{(4!)^2} - \frac{1}{32} + \frac{1}{16} \right) + \O{x^{10}} \notag \\ &= 1 - \frac{x^2}{2} + \frac{5 x^4}{24} - \frac{61 x^6}{720} + \frac{277 x^8}{8064} + \O{x^{10}} \end{align}
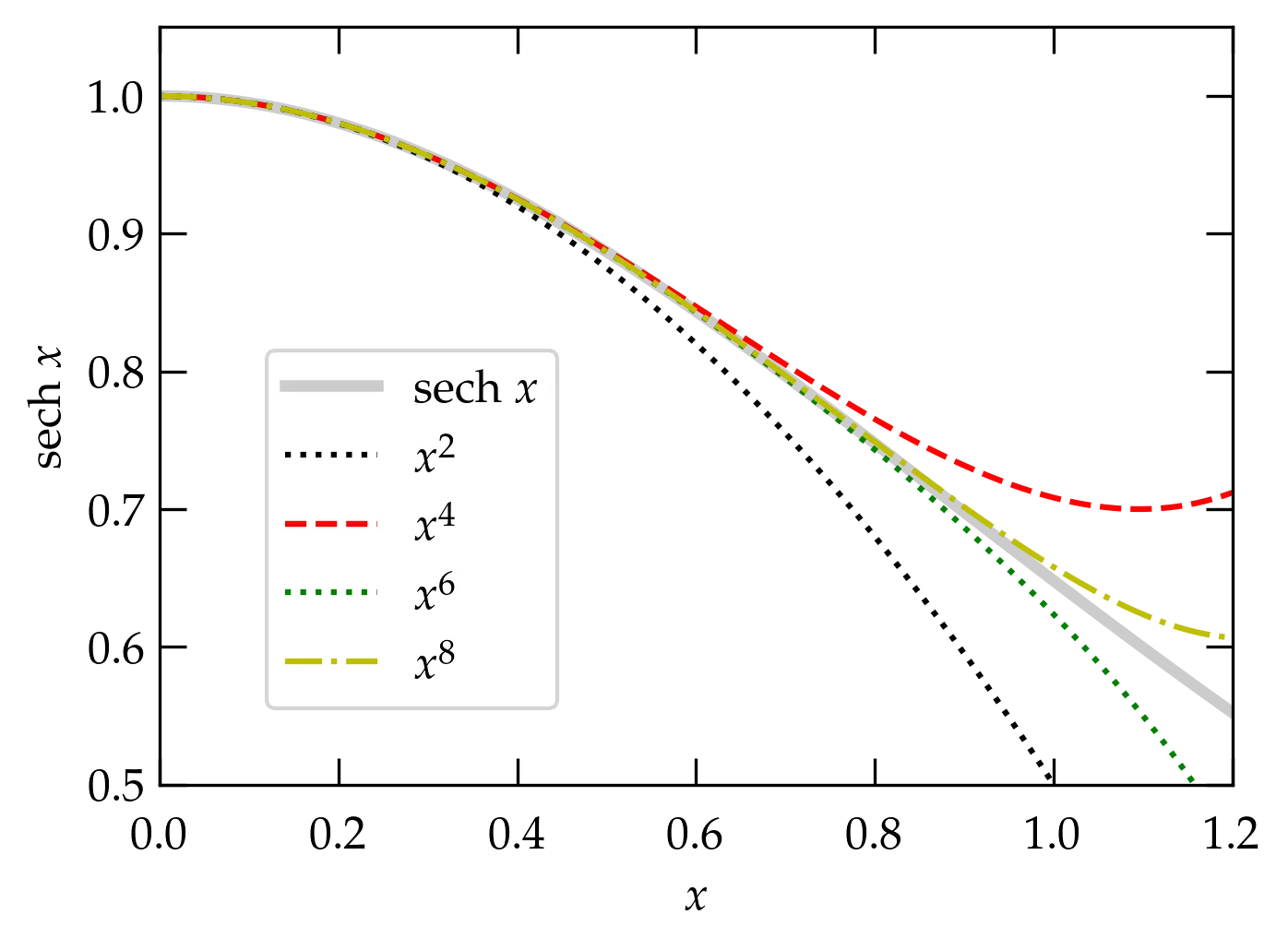
Figure 1 — Maclaurin series for the hyperbolic cosine obtained by inverting the series for \(\cosh x\). Each successive curve includes the terms through the order listed in the legend.
See the page on Euler’s \(\Gamma\) function for an illustration of the power of series expansion as a means of obtaining an analytic expression for the factorial function.
Derive a power series expansion through \(x^5\) for \(\cot x\) by dividing the series for \(\cos x\) by the series for \(\sin x\). Ans: \[ \cot x = \frac1x - \frac{x}{3} - \frac{x^3}{45} - \frac{2 x^5}{945} + \cdots \] Note that this series includes a negative power of \(x\), which means it is not a Taylor series. Series that include negative powers are called Laurent series and are very common in the theory of functions of a complex variable.
The derivative of \(\tan^{-1}x\) is \((1+x^2)^{-1}\). By integrating, find a series expansion for \(\tan^{-1} x\).
One way to compute a series for \(\sin^{-1} x\) is to start with \(x = \sin y\). Then \(\dv{x}{y} = \cos y = \sqrt{1-x^2}\), or \(\dv{y}{x} = 1/\sqrt{1-x^2}\).