
You have all been introduced to the field theory of electromagnetism, developed by Faraday, Amp¸re, Gauss, and Maxwell, among others, and put in roughly modern form at the end of the nineteenth century by Oliver Heaviside. Your previous exposure probably emphasized the integrated form of the Maxwell equations: Gauss's law of electrostatics and Amp¸re's circuital law of magnetostatics.
It may come as a significant relief to you to know up front that
those relations
The first part of the course focuses on electrostatics and the solution of Laplace's and Poisson's equations in various coordinate systems and with various boundary conditions. Rather than focusing on the electric field (a vector), we work primarily with the electrostatic potential V, which is a scalar. Important concepts from this portion of the course are the uniqueness theorem (which guarantees that for suitable and physical boundary conditions, V is unique), the method of images (a form of guess-and-check), the separation of variables approach to solving Laplace's equation, and the multipole expansion of the potential of a localized arrangement of charges. Besides deepening your understanding of electric phenomena, these investigations will help you build an intuition for the solutions to Laplace's and Poisson's equations, which arise not only in electromagnetism but also in quantum mechanics, acoustics, fluid mechanics, heat transport, and a variety of other physical systems.
The course then proceeds to examine the effect of matter on static electric fields, exploring the behavior of dielectrics and the interaction of the charges inside macroscopic chunks of matter with external charges and/or applied electric fields. We will also consider static magnetic fields and materials in analogous fashion.
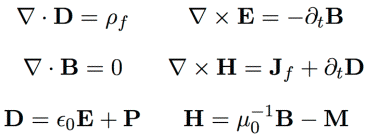
The final portion of the course will address electrodynamics and the fundamentals of electromagnetic radiation. We will discuss Fresnel's treatment of reflection and refraction, and possibly its generalization to nonlinear media. Depending on time and interest, we may touch on near-field optics, wave guides, photonic bandgaps, and other modern topics.
Physics 151 meets MWF at 10 in Thomas-Garrett 103 (although there may be a room swap with Prof. Sparks--stay tuned). In general, the Friday meeting will function as a recitation; if possible, we will divide the class into two groups, one of which meets at the 11 o'clock slot. Homework will normally be due on Fridays at the beginning of the hour.
Grades will be based on homework, two midterms, and a final exam, in approximately the following proportions:
Drop by any time to talk about the course, send me e-mail messages, or phone. Office hours to be established once I have a chance to establish your preferences.
I invite and request your help in making sure that the pace of the course is satisfactory, the homework useful and not too time-consuming, and the explanations clear. I welcome feedback in class and outside of class, I encourage you to visit me in the office.
Physics 151 is a mathematical physics course, but it is important to write solutions that combine mathematics with verbal explanation and justification of the assumptions that you make. Please treat the graders with respect: don't try to put one over on them.
Jeff Jauregui and Steven Avery have graciously consented to grade the course. Please endeavor to make their efforts as straightforward as possible. The purpose of homework is, of course, for you to work with the concepts and techniques of the course, and gain some facility in their application. If you should perchance stray on a problem, please do not rely on the grader to discern just where your solution went south. Rather, take advantage of the provided solution. If the divergence is still unclear, by all means come to discuss the problem with me.
I encourage you to collaborate with one another. By now everyone should recognize that the hard part of most physics problems is the setup, not grinding through the mathematics. Accordingly, you should struggle with the setup before seeking advice from colleagues.
Peter Saeta, Keck 1247, x 73939, saeta@hmc.edu
© 2003 Peter N. Saeta; last updated 8/26/03.